| Conectiva | Notación | Ejemplo de uso | Análogo natural | Ejemplo de uso en el lenguaje natural | Tabla de verdad |
|---|---|---|---|---|---|
| Negación |  |  | no | No está lloviendo. |  |
| Conjunción |  | 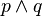 | y | Está lloviendo y es de noche. |  |
| Disyunción | 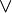 |  | o | Está lloviendo o es de noche. |  |
| Condicional material |  |  | si... entonces | Si está lloviendo,entonces es de noche. |  |
| Bicondicional |  |  | si y sólo si | Está lloviendo si y sólo si es de noche. |  |
| Negación conjunta |  |  | ni... ni | Ni está lloviendo nies de noche. | 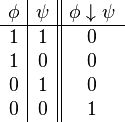 |
| Disyunción excluyente] | 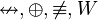 |  | o bien... o bien | O bien está lloviendo,o bien es de noche. | 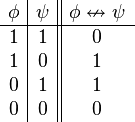 |
[editar]Otras conectivas
Dado que las conectivas son funciones de verdad, existirán tantas conectivas como funciones de verdad. Sin embargo, no todas las funciones de verdad tienen análogos en el lenguaje natural, y en consecuencia, no todas son estudiadas con el mismo interés. A continuación se incluye una tabla que lista las 18 conectivas binarias posibles.

Donde:
 es una tautología.
es una tautología.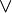 es la disyunción.
es la disyunción. es el condicional material inverso.
es el condicional material inverso.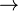 es el condicional material.
es el condicional material. es el bicondicional.
es el bicondicional. es la conjunción.
es la conjunción. es la negación alternativa, incompatibilidad, o "NAND".
es la negación alternativa, incompatibilidad, o "NAND".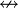 es la disyunción exclusiva, contravalencia o "XOR".
es la disyunción exclusiva, contravalencia o "XOR".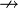 es la negación del condicional material.
es la negación del condicional material. es la negación del condicional inverso.
es la negación del condicional inverso. es la negación conjunta, o "NOR".
es la negación conjunta, o "NOR".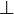 es una contradicción.
es una contradicción.
La Negación
La operación unitaria de negación, no es cierto que se representa por “¬” y tiene la siguiente tabla de verdad de verdad
| p | ¬p |
| V | F |
| F | V |
Ejemplo. Encuentre la negación de las expresiones siguientes:
) Algún elefante es de color rosa
v) Ningún pez respira fuera del agua
vi) Todos los leones son feroces
v) Ningún pez respira fuera del agua
vi) Todos los leones son feroces
Solución:
) Ningún elefante es de color rosa
v) Algún pez respira fuera del agua
vi) Algún león no es feroz
v) Algún pez respira fuera del agua
vi) Algún león no es feroz
Nota: Las tres últimas proposiciones se derivan de proposiciones abiertas que veremos en la sección 1.4 Calculo de Predicados Definición.
La conjunción de las proposiciones p, q es la operación binaria que tiene por resultado p y q, se representa por p^q, y su tabla de verdad es:
| p | q | p^q |
|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
La conjunción nos sirve para indicar que se cumplen dos condiciones simultánea mente, así por ejemplo si tenemos:
La función es creciente y está definida para los números positivos, utilizamos
p ^ q, donde
p: la función es creciente
q: la función esta definida para los números positivos
Así también: p ^ q, donde
q: la función esta definida para los números positivos
Así también: p ^ q, donde
p: el número es divisible por 3
q: el número está representado en base 2
q: el número está representado en base 2
se lee: El número es divisible entre 3 y está representado en base 2.
Nota: Observamos que para la conjunción p ^ q sea verdadera las dos expresiones que intervienen deben ser verdaderas y sólo en ese caso como se indica por su tabla de verdad.
La disyunción de dos proposiciones p, q es la operación binaria que da por resultado p ó q, notación p v q, y tiene la siguiente tabla:
| p | q | p v q |
|---|---|---|
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
Con la disyunción a diferencia de la conjunción, representamos dos expresiones y que afirman que una de las dos es verdadera, por lo que basta con que una de ellas sea verdadera para que la expresión p ∨ q sea verdadera.
Así por ejemplo la expresión: el libro se le entregará a Juan o el libro se le entregará a Luis significa que si va uno de los dos, el libro se le entrega, si van los dos también se entrega y solamente en caso de que no vaya ninguno de los dos no se debe entregar.
Aquí debemos tener cuidado, porque en español muchas veces utilizamos la disyunción para representar otros operadores que aparentemente son lo mismo, pero que tienen diferente significado.
En español tenemos tres casos de disyunción:
La llamada y/o bancaria, lógica o matemática, que es la misma y se utiliza en computación como el operador OR, este operador corresponde al mencionado anteriormente p v q y ya se mostró su tabla de verdad.
La o excluyente, que algunos también le llaman o exclusiva, y que indica que una de las dos proposiciones se cumple, pero no las dos. Este caso corresponde por ejemplo a: Hoy compraré un libro o iré al cine; se sobrentiende que una de las dos debe ser verdadera, pero no la dos. Se representa por p XOR q y su tabla de verdad es:
| p | q | p XOR q |
|---|---|---|
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
Por último, también es muy común utilizar una disyunción como la siguiente: El menú incluye café o té. En este caso se esta dando una disyuntiva diferente pues no se pueden las dos simultánea mente como en el caso anterior, pero aquí si es válido el caso donde las dos son falsas. Es el caso “no ámbas”, se puede representar por p § q y su tablas es
| p | q | p § q |
|---|---|---|
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | V |
Nota: El último símbolo no es estándar y puede haber varias formas de representarlo.
Un buen ejercicio consiste en enunciar varias expresiones del español que utilizando los conectivos y o para analizar cuál de los operadores es.
Hay que tener mucho cuidado cuando se traduce del lenguaje usual por las costumbres, muchas veces depende del contexto o de la situación específica en la que se usan los conectivos, por ejemplo si decimos: Se pueden estacionar alumnos y maestros, en realidad se está queriendo decir un operador disyuntivo, en este caso la o matemática, o sea el primer operador que corresponde a la primera tabla de esta sección.
La condicional de dos proposiciones p, q da lugar a la proposición; si p entonces q, se representa por p → q, y su tabla de verdad está dada por:
| p | q | p→q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
Con respecto a este operador binario, lo primero que hay que destacar es que no es conmutativo, a diferencia de los dos anteriores la conjunción y la disyunción. El único caso que resulta falso es cuando el primero es verdadero y el segundo falso.
Por ejemplo, si p es llueve y q es hay nubes entonces:
p → q es si llueve entonces hay nubes.
También cabe señalar que este viene a ser el operador más importante en el proceso deductivo y que la mayoría de las leyes de inferencia y las propiedades en matemáticas se pueden enunciar utilizando este operador.
La bicondicional de dos proposiciones p, q da lugar a la proposición; p si y sólo si q, se representa por p ↔ q su tabla de verdad está dada por:
| p | q | p ↔ q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | V |
Jerarquía de Operadores.
Combinando los operadores anteriores podemos formar nuevas expresiones.
En términos formales la negación de p, deberá ser ( ¬ p), así como la conjunción de p y q sería (p ^ q). Con el uso de paréntesis evitamos la ambiguedad, por ejemplo ¬p ^ q podría significar dos cosas distintas
Por un lado podría significar: (( ¬ p) ^ q) O también: ( ¬ (p ^ q)).
En la práctica para no usar tantos paréntesis se considera que el operador ¬ tiene jerarquía sobre ^, v, →, ↔. Así ¬ p ^ q significa (( ¬ p)^ q).
En algunos casos se considera ^, v tienen mayor jerarquía que ↔ por lo que p ↔ q v r sería (p ↔ (q v r)) y también que ^ tiene prioridad sobre v, por lo que p ^ q v r sería (p ^ q) v r.
Así por ejemplo, en electrónica, para representar circuitos lógicos se utiliza + en lugar de v y · en lugar de ^.
Por lo que p·q+r es ((p ^ q) v r).
En estos apuntes no se considerará jerarquía en ninguno de los operadores binarios ^, v, →, ↔ por lo que utilizaremos paréntesis. Sólo ¬ tiene prioridad sobre los demás operadores. Esto nos ahorra algunos paréntesis, por ejemplo: ((( ¬ p) ^ q) v r) se representa por ( ¬ p ^ q) v r.
Contrucción de Tablas de Verdad
Como ya sabemos la sintaxis en lógica es la forma correcta de escribir una fórmula y la semántica es lo que significa. Como en lógica solamente tenemos dos valores una fórmula solamente puede ser verdadera o falsa. Para determinar su valor seguimos las reglas simples que dimos en las definiciones básicas de acuerdo a su tabla de verdad. Esto lo hacemos mediante interpretaciones. Una interpretación de una fórmula es un conjunto de valores que se les asignan a sus proposiciones atómicas.
Al interpretar una fórmula lo que finalmente vamos a obtener es un valor de verdad, bien sea verdadero o falso. Pero para poder encontrarlo muchas veces el proceso en laborioso porque puede estar formada por varias proposiciones atómicas. Primeramente se le asignan valores de verdad a los átomos y se puede encontrar el valor de la expresión.
Si deseamos hacerlo en general, debemos analizar todas las posibilidades, esto se puede hacer construyendo una tabla de verdad. Para fines prácticos cuando se tienen varios átomos las tablas de verdad no resultan prácticas por lo que analizaremos solamente expresiones con tres átomos como máximo.
Por supuesto que se puede construir una tabla para un número mayor de átomos, pero notemos que por cada átomo que se aumente el número de renglones se duplica. Esto es, para un átomos son dos renglones, para dos átomos son cuatro, para tres átomos son ocho, para cuatro dieciséis, etc.
Algoritmo para construir una tabla de verdad de una fórmula en lógica de proposiciones.
1. Escribir la fórmula con un número arriba de cada operador que indique su jerarquía. Se escriben los enteros positivos en orden, donde el número 1 corresponde al operador de mayor jerarquía. Cuando dos operadores tengan la misma jerarquía, se le asigna el número menor al de la izquierda.
2. Construir el árbol sintáctico empezando con la fórmula en la raíz y utilizando en cada caso el operador de menor jerarquía. O sea, del número mayor al menor.
3. Numerar las ramas del árbol en forma secuencial empezando por las hojas hacia la raíz, con la única condición de que una rama se puede numerar hasta que estén numerados los hijos. Para empezar con la numeración de las hojas es buena idea hacerlo en orden alfabético, así todos obtienen los renglones de la tabla en el mismo orden para poder comparar resultados.
4. Escribir los encabezados de la tabla las fórmulas siguiendo la numeración que se le dio a las ramas en el árbol sintáctico.
5. Asignarle a los átomos, las hojas del árbol, todos los posibles valores de verdad de acuerdo al orden establecido. Por supuesto que el orden es arbitrario, pero como el número de permutaciones es n!, conviene establecer un orden para poder comparar resultados fácilmente.
6. Asignar valor de verdad a cada una de las columnas restantes de acuerdo al operador indicado en el árbol sintáctico utilizando la tabla de verdad correspondiente del Tema 1.3 Conexiones Lógicas y Jerarquías. Conviene aprenderse de memoria las tablas de los operadores, al principio pueden tener un resumen con todas las tablas mientras se memorizan.
7. La última columna, correspondiente a la fórmula original, es la que indica los valores de verdad posibles de la fórmula para cada caso.
Ejemplo. Construya la tabla de verdad de las siguientes expresiones lógicas:
) ¬(p ¬ q) → ¬ r
v) (¬p ^ q) → ¬(q v ¬r)
v) (¬p ^ q) → ¬(q v ¬r)
Solución:
i) Seguimos los pasos del algoritmo con la fórmula (p → ¬q) v (¬p v r)
1. Vemos que los operadores de los paréntesis tienen mayor jerarquía, empezamos por el paréntesis izquierdo por lo que la fórmula con jerarquías marcadas sería:
2. Construir el árbol Sintáctico empezando a descomponer por el operador con el número mayor, seguir en orden descendiente hasta el último que es el que tiene el número 1.
3. Numerar las ramas del árbol
4. Escribir los encabezados de la tabla utilizando las fórmulas en el árbol siguiendo la numeración del paso 3.
5. Asignar valores de verdad a los átomos, en este caso, las tres primeras columas.
| 1 | 2 | 3 |
| p | q | r |
| V | V | V |
| V | V | F |
| V | F | V |
| V | F | F |
| F | V | V |
| F | V | F |
| F | F | V |
| F | F | F |
6. Asignar los valores de verdad a la ¬ q.
| 1 | 2 | 3 | 4 |
| p | q | r | ¬ q |
| V | V | V | F |
| V | V | F | F |
| V | F | V | V |
| V | F | F | V |
| F | V | V | F |
| F | V | F | F |
| F | F | V | V |
| F | F | F | V |
7. Asignar los valores de verdad a la ¬ p.
| 1 | 2 | 3 | 4 | 5 |
| p | q | r | ¬ q | ¬ p |
| V | V | V | F | F |
| V | V | F | F | F |
| V | F | V | V | F |
| V | F | F | V | F |
| F | V | V | F | V |
| F | V | F | F | V |
| F | F | V | V | V |
| F | F | F | V | V |
8. Asignar los valores de verdad basados en la tabla de la condicional con p(condición 1) → ¬q(condición 4).
| 1 | 2 | 3 | 4 | 5 | 6 |
| p | q | r | ¬ q | ¬ p | p → ¬q |
| V | V | V | F | F | F |
| V | V | F | F | F | F |
| V | F | V | V | F | V |
| V | F | F | V | F | V |
| F | V | V | F | V | V |
| F | V | F | F | V | V |
| F | F | V | V | V | V |
| F | F | F | V | V | V |
9. Asignar los valores de verdad basados en la tabla disyunción con la ¬p(condición 4) v r(condición 3).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p | q | r | ¬ q | ¬ p | p → ¬q | ¬p v r |
| V | V | V | F | F | F | V |
| V | V | F | F | F | F | F |
| V | F | V | V | F | V | V |
| V | F | F | V | F | V | F |
| F | V | V | F | V | V | V |
| F | V | F | F | V | V | V |
| F | F | V | V | V | V | V |
| F | F | F | V | V | V | V |
10. Completar el resto de las condiciones utilizando las definiciones de los operadores,p → ¬q (condición 6), v, ¬p v r (condición 7).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| p | q | r | ¬ q | ¬ p | p → ¬q | ¬p v r | (p → ¬q) v (¬p v r) |
| V | V | V | F | F | F | V | V |
| V | V | F | F | F | F | F | F |
| V | F | V | V | F | V | V | V |
| V | F | F | V | F | V | F | V |
| F | V | V | F | V | V | V | V |
| F | V | F | F | V | V | V | V |
| F | F | V | V | V | V | V | V |
| F | F | F | V | V | V | V | V |
11. La última columna es el resultado da cada interpretación establecida en los primeros tres renglones.
Los demás problemas son similares y se obtienen las tablas siguientes.
FALTA PONER LOS ÁRBOLES SINTÁCTICOS DE LOS EJEMPLOS 2 AL 5.
| 1 | 2 | 3 | 4 | 5 |
| p | q | r | q v r | p → (q v r) |
| V | V | V | V | V |
| V | V | F | V | F |
| V | F | V | V | V |
| V | F | F | V | F |
| F | V | V | V | V |
| F | V | F | V | V |
| F | F | V | F | V |
| F | F | F | F | V |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p | q | r | ¬ r | p → ¬ r | q ∨ r | (p → ¬ r) ↔ (q v r) |
| V | V | V | F | F | V | F |
| V | V | F | V | V | V | V |
| V | F | V | F | F | V | F |
| V | F | F | V | V | F | V |
| F | V | V | F | V | V | V |
| F | V | F | V | V | V | V |
| F | F | V | F | V | V | F |
| F | F | F | V | V | F | F |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| p | q | r | ¬ q | p ^ ¬ q | ¬(p ^ ¬q) | ¬ r | ¬(p ^ ¬q) → ¬ r |
| V | V | V | F | F | V | F | F |
| V | V | F | F | F | V | V | V |
| V | F | V | V | V | F | F | V |
| V | F | F | V | V | F | V | V |
| F | V | V | F | F | V | F | F |
| F | V | F | F | F | V | V | V |
| F | F | V | V | F | V | F | F |
| F | F | F | V | F | V | V | V |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| p | q | r | ¬r | ¬p | q v ¬r | ¬p ^ q | ¬(q v ¬r) | (¬p ^ q) → ¬(q v ¬r) |
| V | V | V | F | F | V | F | F | V |
| V | V | F | V | F | V | F | F | V |
| V | F | V | F | F | F | F | V | V |
| V | F | F | V | F | F | F | V | V |
| F | V | V | F | V | V | V | F | F |
| F | V | F | V | V | V | V | F | F |
| F | F | V | F | V | V | F | F | V |
| F | F | F | V | V | V | F | F | V |
CONJUNCIÓN MATEMÁTICA
En matemáticas, el conjugado de un número complejo se obtiene cambiando el signo de su componente imaginaria. Por lo tanto, el conjugado de un número complejo
(donde a y b son números reales) es
El conjugado es a menudo indicado como z * . Aquí, se utiliza la notación 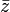 para evitar confusiones con la notación utilizada para indicar la transpuesta conjugada de una matriz (que puede pensarse como una generalización del conjugado de un número). Notar que si el número complejo es tratado como una matriz
para evitar confusiones con la notación utilizada para indicar la transpuesta conjugada de una matriz (que puede pensarse como una generalización del conjugado de un número). Notar que si el número complejo es tratado como una matriz  , las notaciones son idénticas.
, las notaciones son idénticas.
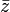 para evitar confusiones con la notación utilizada para indicar la transpuesta conjugada de una matriz (que puede pensarse como una generalización del conjugado de un número). Notar que si el número complejo es tratado como una matriz
para evitar confusiones con la notación utilizada para indicar la transpuesta conjugada de una matriz (que puede pensarse como una generalización del conjugado de un número). Notar que si el número complejo es tratado como una matriz  , las notaciones son idénticas.
, las notaciones son idénticas.Por ejemplo,
Los números complejos pueden ser representados como puntos en un plano con un sistema de coordenadas cartesianas. El eje x contiene los números reales y el eje y contiene los múltiplos de i (la unidad imaginaria). Por lo tanto, en esta representación el conjugado de un número corresponde a su reflexión sobre el eje x.
Sin embargo, en forma polar, el conjugado de reiφ queda determinado por re − iϕ. Lo cual se puede verificar fácilmente aplicando la fórmula de Euler.
Los pares formados por un número y su conjugado son importantes ya que la unidad imaginaria i es indistinta de su inversa aditiva y multiplicativa − i, ya que ambas satisfacen la definición de la unidad imaginaria: x2 = − 1. Lo más común es que, si un número complejo es solución de un problema, también su conjugado lo es, esto se verifica por ejemplo en las soluciones complejas de la fórmula cuadrática con coeficientes reales.
Estas propiedades se aplican a todos los números complejos z y w, a menos que se indique lo contrario.
 si w es distinto de cero
si w es distinto de cero
 si y solo si z es real
si y solo si z es real
 para todo entero n
para todo entero n
 si z es distinto de cero
si z es distinto de cero
Esta última fórmula es el método normalmente utilizado para encontrar el inverso de un número complejo si el número está expresado en coordenadas rectangulares.
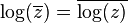 si z es distinto de cero
si z es distinto de cero
- Disyunción inclusiva y exclusiva
 La formalización de enunciados del lenguaje natural no tiene especial dificultad en el caso de la disyunción, aunque sí hay algunas sutilezas con las que conviene familiarizarse.Como hemos dicho, la disyunción "p
La formalización de enunciados del lenguaje natural no tiene especial dificultad en el caso de la disyunción, aunque sí hay algunas sutilezas con las que conviene familiarizarse.Como hemos dicho, la disyunción "p q" será verdadera en caso de que p sea verdadera, o q sea verdadera, o tanto p como q sea verdadera: se trata de la disyunción inclusiva. Siempre que utilicemos en el lenguaje natural la conjunción disyuntiva "o" en este sentido, utilizaremos el símbolo "
q" será verdadera en caso de que p sea verdadera, o q sea verdadera, o tanto p como q sea verdadera: se trata de la disyunción inclusiva. Siempre que utilicemos en el lenguaje natural la conjunción disyuntiva "o" en este sentido, utilizaremos el símbolo " ".Los ejemplos que hemos venido viendo hasta este momento se basan en esta interpretación inclusiva de la disyunción. Por ejemplo, cuando decimos que para optar a un puesto de trabajo hay que saber inglés o francés, interpretamos que alguien que sabe inglés puede optar a dicho trabajo, alguien que sabe francés también, y, por supuesto, alguien que sepa tanto inglés o francés también.Pero también existe la llamada disyunción exclusiva, que viene a decir que al menos una de las opciones es verdadera, pero sólo una. En este sentido exclusivo, si en "p
".Los ejemplos que hemos venido viendo hasta este momento se basan en esta interpretación inclusiva de la disyunción. Por ejemplo, cuando decimos que para optar a un puesto de trabajo hay que saber inglés o francés, interpretamos que alguien que sabe inglés puede optar a dicho trabajo, alguien que sabe francés también, y, por supuesto, alguien que sepa tanto inglés o francés también.Pero también existe la llamada disyunción exclusiva, que viene a decir que al menos una de las opciones es verdadera, pero sólo una. En este sentido exclusivo, si en "p q", p es verdadera y q también lo es, la disyunción exclusiva es falsa.Por ejemplo, en el lenguaje natural empleamos este sentido exclusivo de la disyunción cuando decimos que alguien es cristiano o musulmán. Si alguien es cristiano, si es consecuente con ello no podrá ser musulmán, y viceversa. O cuando decimos que un examen se aprueba o se suspende.En este caso se utiliza el símbolo "
q", p es verdadera y q también lo es, la disyunción exclusiva es falsa.Por ejemplo, en el lenguaje natural empleamos este sentido exclusivo de la disyunción cuando decimos que alguien es cristiano o musulmán. Si alguien es cristiano, si es consecuente con ello no podrá ser musulmán, y viceversa. O cuando decimos que un examen se aprueba o se suspende.En este caso se utiliza el símbolo " " o bien el símbolo "
" o bien el símbolo " ". La tabla de verdad de la disyunción exclusiva sería la siguiente:
". La tabla de verdad de la disyunción exclusiva sería la siguiente:
p
q
p  q
q
V
V
F
V
F
V
F
V
V
F
F
F En este trabajo utilizaremos solamente la disyunción en sentido inclusivo. Hay que hacer notar que la disyunción exclusiva puede definirse utilizando las siguientes combinaciones de negación, conjunción y disyunción, es decir, "p q" equivale a cualquiera de las siguientes expresiones:
q" equivale a cualquiera de las siguientes expresiones:- (p
 q)
q) ¬(p
¬(p q)
q) - (p
 ¬q)
¬q) (¬p
(¬p q)
q) - ¬(p
 q)
q) ¬(¬p
¬(¬p ¬q)
¬q)
- (p











Es muy importante , pero no halle lo que yo queria encontrar.
ResponderEliminaryo tampoco, buscaba negacion alternativa
ResponderEliminarEsta bien pero no encontré lo que buscaba que era colectivo de conjunción y tabla de verdad
ResponderEliminarGracias en mi caso si encontré lo que buscaba lindo dia
ResponderEliminarMuchas gracias en mi caso si encontré lo que buscaba
ResponderEliminarmuy util para lo que requiero, muchas gracias por compartir
ResponderEliminar