BIBLIOGRAFIAS

http://www.mitecnologico.com/Main/Proposiciones
http://es.wikipedia.org/wiki/Cuantificador_universal
http://es.wikipedia.org/wiki/Implicaci%C3%B3n
http://campusvirtual.unex.es/cala/epistemowikia/index.php?title=Contradicci%C3%B3n_L%C3%B3gica

PROPOSICIONES MATEMATICAS

En el idioma científico, una proposiciòn se refiere a un enunciado que puede ser verdadero o falso, generalmente una oración enunciativa, base de lo que constituye el lenguaje formal de la lógica simbólica.

Una proposición lógica es Expresión enunciativa a la que puede atribuirse un sentido o función lógica de verdad o falsedad.

Aunque existen lógicas polivalentes, en orden a la claridad del concepto, aquí consideramos únicamente el valor de Verdad o Falsedad.

Otro tipo de entes que se utilizan en computación que también está asociado a “dos” opciones, es lo que se conoce como expresiones booleanas. Estas expresiones, que deben su nombre a George Boole, se pueden ver caracterizadas como verdaderas ó falsas y de acuerdo a esta condición se desarrolla el estudio sobre dichos conceptos. Este tema se conoce como cálculo de proposiciones.

Un enunciado lingüístico (generalmente en la forma gramatical de una oración enunciativa) puede ser considerado como proposición lógica cuando es susceptible de ser verdadero o falso. “Es de noche”.Son A ,Ante ,bajo ,con ,contra ,de ,desde ,durante ,en ,entre ,hacia ,hasta ,para ,por ,segun ,sin ,sobre y tras

Los argumentos son una de las formas más comunes en matemáticas, en lógica y en computación de establecer razonamientos para llegar a la verdad. Si tenemos un conectivo lógico OR de dos valores de entrada y después un inversor, cuál es la salida. O si en un programa con una instrucción tipo if se tiene la condición X > 3 and X < 10 cómo se sabe si se ejecutó el comando.

Desarrollo.

La lógica matemática es la disciplina que trata de métodos de razonamiento. En un nivel elemental, la lógica proporciona reglas y técnicas para determinar si es o no valido un argumento dado. El razonamiento lógico se emplea en matemáticas para demostrar teoremas; en ciencias de la computación para verificar si son o no correctos los programas; en las ciencias física y naturales, para sacar conclusiones de experimentos; y en las ciencias sociales y en la vida cotidiana, para resolver una multitud de problemas. Ciertamente se usa en forma constante el razonamiento lógico para realizar cualquier actividad.

Proposiciones y operaciones lógicas.

Una proposición o enunciado es una oración que puede ser falsa o verdadera pero no ambas a la vez. La proposición es un elemento fundamental de la lógica matemática.

A continuación se tienen algunos ejemplos de proposiciones válidas y no válidas, y se explica el porqué algunos enunciados no son proposiciones. Las proposiciones se indican por medio de una letra minúscula, dos puntos y la proposición propiamente dicha. Ejemplo.

p: La tierra es plana.

q: −17 + 38 = 21

r: x > y-9

s: El Morelia será campeón en la presente temporada de Fut-Bol.

t: Hola ¿como estas?

w: Lava el coche por favor.

Los incisos p y q sabemos que pueden tomar un valor de falso o verdadero; por lo tanto son proposiciones validas. El inciso r también es una proposición valida, aunque el valor de falso o verdadero depende del valor asignado a las variables x y y en determinado momento. La proposición del inciso s también esta perfectamente expresada aunque para decir si es falsa o verdadera se tendría que esperar a que terminara la temporada de fut-boll. Sin embargo los enunciados t y w no son válidos, ya que no pueden tomar un valor de falso o verdadero, uno de ellos es un saludo y el otro es una orden.

Conectivos lógicos y proposiciones compuestas.

Existen conectores u operadores lógicas que permiten formar proposiciones compuestas (formadas por varias proposiciones). Los operadores o conectores básicos son:

Operador and (y)

Se utiliza para conectar dos proposiciones que se deben cumplir para que se pueda obtener un resultado verdadero. Si símbolo es: {Ù, un punto (.), un paréntesis}. Se le conoce como la multiplicación lógica:

Ejemplo.

Sea el siguiente enunciado “El coche enciende cuando tiene gasolina en el tanque y tiene corriente la batería”

Sean:

p: El coche enciende.

q: Tiene gasolina el tanque.

r: Tiene corriente la batería.

De tal manera que la representación del enunciado anterior usando simbología lógica es como sigue:

p = q Ù r

Su tabla de verdad es como sigue:

q r p = q Ù r

1 1 1

1 0 0

0 1 0

0 0 0

Donde.

1 = verdadero

0 = falso

En la tabla anterior el valor de q=1 significa que el tanque tiene gasolina, r=1 significa que la batería tiene corriente y p = q Ù r=1 significa que el coche puede encender. Se puede notar que si q o r valen cero implica que el auto no tiene gasolina y que por lo tanto no puede encender.

Operador Or (o)

Con este operador se obtiene un resultado verdadero cuando alguna de las proposiciones es verdadera. Se eindica por medio de los siguientes símbolos: {Ú,+,È}. Se conoce como las suma lógica. Ejemplo.

Sea el siguiente enunciado “Una persona puede entrar al cine si compra su boleto u obtiene un pase”. Donde.

p: Entra al cine.

q: Compra su boleto.

r: Obtiene un pase.

q r p = q Ù r

1 1 1

1 0 0

0 1 0

0 0 0

q r

La única manera en la que no puede ingresar al cine (p=0), es que no compre su boleto (q=0) y que no obtenga un pase (r=0).

p =q Ú r

1 1 1

1 0 1

0 1 1

0 0 0

Operador Not (no)

Su función es negar la proposición. Esto significa que sí alguna proposición es verdadera y se le aplica el operador not se obtendrá su complemento o negación (falso). Este operador se indica por medio de los siguientes símbolos: {‘, Ø,-}. Ejemplo.

La negación de está lloviendo en este momento (p=1), es no está lloviendo en este momento (p’=0)

p p’

1 0

0 1

Además de los operadores básicos (and, or y not) existe el operador xor, cuyo funcionamiento es semejante al operador or con la diferencia en que su resultado es verdadero solamente si una de las proposiciones es cierta, cuando ambas con verdad el resultado es falso.

En este momento ya se pueden representar con notación lógica enunciados más complejos. Ejemplo

Sean las proposiciones:

p: Hoy es domingo.

q: Tengo que estudiar teorías del aprendizaje.

r: Aprobaré el curso.

El enunciado: “Hoy es domingo y tengo que estudiar teorías de aprendizaje o no aprobaré el curso”. Se puede representar simbólicamente de la siguiente manera:

p Ù qÚ r

Por otro lado con ayuda de estos operadores básicos se pueden formar los operadores compuestos Nand (combinación de los operadores Not y And), Nor (combina operadores Not y Or) y Xnor (resultado de Xor y Not). PROPOSICIONES.

Como se menciono en el capitulo anterior, en computación se utiliza la representación binaria porque aparecen solo dos elementos distintos. El trabajar con solo 2 opciones facilita la implementación de los conceptos.

Otro tipo de entes que se utilizan en computación también esta asociado a “dos” opciones, es lo que se conoce como expresiones booleanas.

Estas expresiones, que deben su nombre a George Boole, se pueden ver caracterizadas como verdaderas ó falsas y de acuerdo a esta propiedad se desarrolla el estudio sobre dichos conceptos.

Empezaremos por clasificar las expresiones del lenguaje, distinguiendo lo que se puede considerar entre las experiencias booleanas y las que no.

EXPRESIONES:

Proposiciones lógicas

EXPRESIONES

BOLEANAS: Proposiciones abiertas

                           Frases indeterminadas

PROPOSICIÓN LÓGICA.

Es cualquier expresión que puede ser verdadera o falsa pero nunca ambas.

PROPOSICIÓN ABIERTA

Una expresión que contiene una o mas variables y al sustituir las variables por valores específicos se obtienen una proposición lógica.

FRASES

Son las que no sean proposiciones lógicas o proposiciones abiertas son frases.

Ejemplo

i) México está en América	Proposición Lógica
ii) 1 < 2	Proposición Lógica
iii) Hoy es lunes	Proposición Abierta
iv) x+3=5	Proposición Abierta
v) Ecosistemas	Frase
vi) Buenos días	Frase
vii) El 3 de abril de 1970 fué domingo	Proposición Lógica
viii) Los cocodrilos pueden volar	Proposición Lógica
ix) Las matemáticas son agradables	Proposición Abierta
x) Esta expresión es falsa	Frase

LOS CUANTIFICADORES

DEFINICIÒN

En lógica matemática, se usa el símbolo , denominado cuantificador universal, antepuesto a unavariable para decir que "para todo" elemento de un cierto conjunto se cumple la proposición dada a continuación. En texto se puede representar con el carácter ∀.

Normalmente, en lógica, el conjunto al que se refiere es el universo o dominio de referencia, en el cual aparecen todas las constantes.

Ejemplo

Si tenemos dos conjuntos diferentes A y B, y Aes un subconjunto de B:

Todo elemento x de A pertenece a B:

Al ser A y B conjuntos diferentes como indica el diagrama, podemos decir que no todos los elementos y de B pertenecen a A, siendo esto una garantia suficiente para que dos conjuntos cualesquiera puedan ser diferentes:

Es decir, que no para todo elemento y de B tenemos que o implica que y también pertenezca a A.

Relación cuantificador universal y el cuantificador existencial

Dada una expresión P(x), según el cuantificador universal se puede transformar en otra equivalente con el cuantificador existencial:

que podriamos leer: si para todo x se cumple P(x) no existe un x que no cumpla P(x).

Según el ejemplo anterior:

Para todo x que pertenece a A implica que x pertenece a B, que podemos expresar:

No existe un x de B por tanto x no este en a A.

Cuantificador existencial

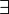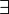En el lenguaje de predicados en lógica matemática, se usa el símbolo: , llamado cuantificador existencial, antepuesto a una variable para decir que "existe" al menos un elemento del conjunto al que hace referencia la variable, que cumple la proposición escrita a continuación.

Normalmente, en lógica, el conjunto al que se hace referencia es el universo o dominio de referencia, que está formado por todas las constantes.

Ejemplo

Si tenemos dos conjuntos diferentes A y B, y Aes un subconjunto de B:

existe al menos un elemento x de B que pertenece a A:

Al afirmar que existe al menos un x que pertenece a B y pertenece a A, quiere decir que no todos los elementos de B pertenecen a A, al ser A y B conjuntos distintos, existe al menos un elemnto y de B que no pertenece a A:

Que podemos leer: existe al menos un elemento y en B, y este elemento y no pertenece a A.

IMPLICACIÒN MATEMATICA Y TAUTLOGIA

Implicación

Para otros usos de este término, véase compromiso.

Etimológicamente del latín “in ─ plicare”, significa el hecho de algo que está “plegado” o doblado en el interior de algo que oculta lo que hay en su interior que, por tanto, aunque está, no es visible o perceptible.

Su contraposición se manifiesta en el término latino “ex ─ plicare”. La “explicación” es el hecho de desplegar lo que está plegado; sacar al exterior, hacer visible, o comprensible, aquello que está “implicado” en el interior de algo que lo hacía oculto o no comprensible.

La realidad del mundo como un orden implicado

La realidad del mundo no se nos manifiesta como un conjunto de cosas o de hechos aislados, sino que, por el contrario, aparece como un proceso, como un conjunto de hechos y de cosas relacionados entre sí de forma que unas cosas "dependen" de otras, unos hechos "suceden" a otros, o suceden "siempre y cuando" se dé un "orden" entre determinadas circunstancias etc. etc.

Estas relaciones en las que unas cosas dependen de otras, o unos hechos suceden a otros, solemoscomprenderlas, de forma general, bajo la idea de causa.¹

El conocimiento del mundo lo elaboramos a través de unos datos captados por los sentidos; y lo manejamos conceptual y lingüísticamente y lo comunicamos a los demás según interpretamos la realidad y "creemos" que conocemos el mundo como realidad.

Esta creencia en el modo de conocer el mundo como relación de causas, la expresamos en el pensamiento y el lenguaje mediante las oraciones condicionales que en lógica se formalizan lingüísticamente como:

"Si llueve el suelo está mojado"

"Cuando llueve el suelo está mojado"

"Siempre que llueve el suelo está mojado"

"Llueve, luego el suelo está mojado"

"Llueve, por tanto, el suelo está mojado" etc.

Que de forma general vienen a decir que:

"El suelo está mojado porque llueve"

"La lluvia causa que el suelo esté mojado"

"El suelo está mojado a consecuencia de la lluvia"

"Todas las lluvias mojan el suelo"

Y cualquier otra expresión o enunciado que establezca como significado "unas relaciones semejantes".

En el cálculo lógico de deducción natural este tipo de expresiones se formalizan simbólicamente como: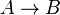 que se interpretan como más adelante se explica; siendo A causa o conjunto de causas y B efecto o conjunto de efectos.

Al percibir algunas cosas o algunos hechos, "esperamos", "creemos", que van a suceder otras; o "suponemos" que estas cosas suceden porque antes han sucedido otras. En otras palabras damos por supuesto que unas cosas implican otras y los hechos están implicados unos en otros.

Esta implicación de las cosas y los hechos del mundo suceden no de forma arbitraria sino de forma legal, conforme a leyes. El mundo se nos manifiesta conforme a unas «leyes naturales» según las cuales las cosas suceden así por "necesidad", porque tienen que ser así, y no de forma arbitraria, "por voluntad de los dioses" o el "azar".

Al expresar nuestro conocimiento por medio del lenguaje, utilizamos unas reglas gramaticales y lógicas que, aunque no las conozcamos, las manejamos de forma inconsciente y natural. Pero mediante ellas, creemos que conocemos y expresamos la realidad del mundo.

Pensamos que el conocimiento, cuando es una interpretación adecuada de la realidad, es verdadero. Pero otras veces nos causa admiración cuando sentimos ignorancia.

Pues los hombres comienzan y comenzaron siempre a filosofar movidos por la admiración; al principio, admirados ante los fenómenos sorprendentes más comunes; luego avanzando poco a poco y planteándose problemas mayores, como los cambios de la luna y los relativos al sol, las estrellas y a la generación del universo. Pero el que se plantea un problema o se admira, reconoce su ignorancia, por eso también el que ama los mitos es en cierto modo filósofo, pues el mito se compone de elementos que dejan estupefacto. De suerte que, si filosofaron para huir de la ignorancia, es claro que buscaban el saber en busca del conocimiento, y no por ninguna utilidad

Cuando reflexionamos sobre el fundamento de nuestro conocimiento y que dicho conocimiento es producto de nuestra interactuación con la realidad, puesto que nosotros somos parte de la misma y del mismo proceso, esta reflexión es el fundamento del pensamiento racional que da lugar a la cienciay a la filosofía.

El conocimiento de la ciencia y de la reflexión filosófica supone una gran depuración del conocimiento vulgar. De ahí que la noción de causa, de implicación, de ley científica, la misma noción de experiencia en el contexto científico y filosófico, aunque tengan el mismo fundamento que la noción corriente, requiere un proceso de depuración o formalización para adecuar las nociones lo mejor posible al contenido experimental (que no es lo mismo que la experiencia) de las mismas.

El comprender la realidad del mundo en sus "implicaciones" se hace mediante las "explicaciones" de la ciencia.

La ciencia, por su parte, como pensamiento racional, se somete a unas reglas de razonamiento o funcionamiento de la razón, conocidas, elaboradas y formalizadas, que es lo que normalmente entendemos por lógica y método.

En este artículo consideramos la "implicación" en su sentido meramente lógico. Reservando laexplicación al ámbito de una lógica empírica, que habla del mundo de la experiencia conforme a unmétodo científico y que es lo que consideramos como Ciencia.

La implicación lógica requiere algunas precisiones para su correcta comprensión:

Implicación y Condicional

Aunque en el lenguaje ordinario no suele tener importancia esta distinción, en su sentido lógico y científico las diferencias pueden tener un sentido importante.

Tanto el condicional como la implicación en el cálculo lógico se expresan según el esquema A → B, que puede leerse de dos formas:

Se simboliza	Se lee	Ejemplo
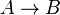	Si   A    entonces    B	"Si hoy es Martes entonces mañana es Miércoles".
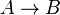	A    implica    B	"Hoy es Martes", por tanto "mañana es Miércoles".

En el primer caso hemos leído un condicional. En el segundo una implicación.

1.- Observamos que, en su escritura, la expresión lingüística difiere de forma fundamental en el uso de las comillas:

"Si A entonces B" es una y única proposición y como tal una única afirmación; por tanto, su interpretación lógica tiene dos valores posibles de verdad, es decir, puede ser verdadera o falsa. Su tabla de valores de verdad nos indica que solamente es falsa en el caso en que “A” sea verdadera y “B” sea falsa; en los demás casos posibles es verdadera. Pero a falta de información complementaria no podemos afirmar ni su verdad ni su falsedad.

En "A implica B" hay dos proposiciones y, por tanto, dos afirmaciones. Pero el valor de cada una es diferente. De modo que afirmando "A", como sentencia verdadera en su contenido semántico, se exige la afirmación de "B" como sentencia verdadera en su contenido semántico. Dicho de otra manera, la afirmación de la segunda depende de la validez de la primera.

2.- Lo condicional es una afirmación hipotética sobre una relación meramente formal. “si se da una condición (antecedente), tiene que darse también lo condicionado (consecuente)”. El hecho de que no se dé la condición no afecta al hecho de que se dé o no se dé lo condicionado.

En la implicación, sin embargo, la relación se establece sobre sentencia en su condición de "contenido semántico". A debería tomarse como afirmación sobre "A"; y B como afirmación sobre "B".

Mientras el condicional es una relación meramente sintáctica, la implicación exige además una relación semántica. En este segundo caso la condición responde a un contenido material.

Así pues implicación debe entenderse como:

La verdad de A exige, o lleva implícita, es decir implicada, la verdad de B.

Lo que nos viene a sugerir que:

Se debe reservar la implicación sólo a los casos en los que la condición es siempre verdadera

Un ejemplo que solemos usar en el lenguaje ordinario puede servir de de ejemplo para lo que intentamos decir.

Cuando alguien está contando algo que el oyente considera una fantasía que no puede ser admitida de ningún modo como verdadera, es frecuente, en español, que el oyente manifieste su incredulidad diciendo: “Si esto es verdad, yo soy el Papa de Roma”.

Si interpretamos dicha expresión como un condicional, entonces la proposición como tal es lógicamente verdadera, puesto que, partiendo de la falsedad del antecedente, el valor de verdad del consecuente no incide en la verdad del condicional como verdad formal, según las tablas de verdad.

Pero si lo interpretamos como una implicación: “Lo que dices” implica que “yo soy el Papa de Roma”, entonces no tiene sentido alguno. Porque “Lo que dices” (como significado) no tiene nada que ver conmigo ni con el Papa de Roma (como significado), y es por tanto un absurdo.

"Si esto es un triángulo entonces la suma de sus ángulos tendrá que ser 180º", es una afirmación hipotética, por tanto débil, mínima, similar en su forma a la anterior. Mientras que "Esto es un triángulo implica que (por tanto) la suma de sus ángulos sea (son) 180º", es una afirmación plena en su contenido.

Para la prueba argumentativa, o derivación formal en un cálculo, basta la afirmación mínima hipotética, por lo que en la práctica del cálculo formal lógico no es necesario tener en cuenta esta distinción, no así en las afirmaciones con pretensión de verdad cuando hablamos del mundo.

Condicional e implicación

Condicional	"Si llueve el suelo está mojado"	Afirmación formal e hipotética, que no habla del mundo
Implicación	"Llueve, por tanto el suelo está mojado"	Afirmación con contenido de verdad y habla del mundo. Equivale materialmente a la afirmación doble: "Llueve"y "el suelo está mojado"

Implicación lógica

La implicación supone un contenido semántico además de formal.

Un sistema lógico se define como una estructura compuesta por un lenguaje formal junto con una relación binaria de consecuencia semántica (o implicación lógica) o una relación binaria de consecuencia sintáctica ├ (derivabilidad), o ambas. La relación de consecuencia semántica se define con respecto a una clase de estructuras y la relación de consecuencia sintáctica, con respecto a un sistema de pruebas.

El cálculo lógico formal sirve para establecer una relación, o derivación entre una condición y su condicionado, o el establecimiento de una afirmación hipotética. Si las premisas son verdaderas lo es también la conclusión.

Cuando el cálculo tiene una intención argumentativa en su contenido semántico, entonces partimos de un contenido material afirmado como verdadero, cuya verdad es condición necesaria de la verdad de lo condicionado en la conclusión, como implicación.

Normalmente el uso lógico del pensamiento es argumentativo en este sentido, y por ello esta distinción no tiene mayor importancia en la vida ordinaria, y suele confundirse con facilidad.

La implicación en la lógica actual

Filón de Megara, hacia el 300 a. de C. estimaba el condicional tal como hoy día se define la función de condicional en las tablas de verdad.

Diodoro de Cronos en la misma época, no aceptaba más que la condición en el sentido de implicación.

Los escolásticos distinguieron entre proposición «formalmente hipotética», la condición y «materialmente hipotética», la implicación, y así ha perdurado en la filosofía tradicional.

En el siglo XIX Frege, Peirce, Russell y, en general los lógicos matemáticos, aceptaron el sentido de Filón, mientras que Clarence Irving Lewis (1883-1964) ha defendido la postura de Diodoro.

Para Lewis la implicación como tal se refiere a la “inferencia” o “prueba”. La condición formal, en cambio, únicamente muestra “lo que ocurriría o podría ocurrir si una proposición falsa fuera verdadera”, lo que abre esta problemática a la cuestión de la «modalidad», (necesidad-contigencia, posibilidad-imposibilidad), especialmente estudiada por este autor, que ha dado lugar a la Lógica modal, de gran desarrollo actualmente.

Un ejemplo explica bien lo que se quiere decir.

El ejemplo antes citado "si esto que dices es verdad, yo soy el Papa de Roma" (A → B), lo consideramos como una afirmación con un contenido de verdad realmente débil, y prácticamente sin sentido.

Sin embargo "si hubieras estado aquí, el asunto se habría resuelto" (A → B), tiene la misma forma sintáctica, pero su contenido semántico de verdad no es comparable al anterior.

Si intentamos encontrar el sentido de verdad contenido en dicha afirmación condicional, observamos:

a) La afirmación parte del conocimiento del contenido semántico falso del antecedente, lo que se manifiesta lingüísticamente en el uso del modo subjuntivo. "Si hubieras estado" → "no has estado".

b) El consecuente es considerado dentro de un "mundo posible", que sabemos que no ha sido real, pero podemos pensar en él como posible,. "Se habría resuelto" → "habría sido posible que se resolviera".

De la misma forma podemos expresar un contenido semántico de verdad basado en la necesidad, como en el caso del triángulo antes citado, o en la afirmación de un deseo, la afirmación de una prescripción etc.

Tal es el campo de la modalidad y la lógica modal.

Definición

Una tautología es un caso especial de proposiciones lógicas caracterizadas por tener exclusivamente el valor verdadero en la columna final de su tabla de verdad, independientemente del valor de las demás proposiciones. Las tautologías son muy comunes, y algunas de ellas muy importantes, tanto, que constituyen leyes o principios lógicos. La validez lógica es justamente el que no puede darse el caso de que siendo verdad el antecedente, no lo sea el consecuente. Todos los argumentos deductivos válidos son tautologías, por definición. Las tautologías son muy importantes en lógica porque son leyes en las que nos podemos apoyar para demostraciones matemáticas. 

Principio de identidad

El principio de indentidad dice que lo que es, es. Formalmente se indica que una proposición P = P. Como se ve en su tabla de verdad, esto es una tautología.

P	P	P = P
V	V	V
F	F	V

Principio del tercio excluido

Formalmente se demuestra que dada una proposición P, esta es verdadera o no es verdadera, pero no puede ser ambas a la vez, es decir, P v ¬P siempre es verdad, por tanto es una tautología. A esta tautología se la conoce como principio del tercio excluido por que entre dos proposiciones que juntas forman una contradicción no existe una tercera posibilidad,es decir, la tercera está excluida.

P	¬P	P v ¬P
V	F	V
F	V	V

Principio de no Contradicción

El principio de no contradicción dice que es imposible que algo sea y no sea en el mismo sentido y en el mismo sujeto, es decir, dada la proposición "P es P" esta siempre será verdadera (tautológica por tanto) pues lo contrario sería caer en una contradicción.

Tautologías más usuales

Las tautologías más conocidas y más usadas en demostraciones matemáticas son las siguientes:

1.- Doble negación.

a). ¬¬p ⇔ p

2.- Leyes conmutativas.

a). (p∨q)⇔(q∨p)

b). (p∧q)⇔(q∧p)

c). (p↔q)⇔(q↔p)

3.- Leyes asociativas.

a). [(p∨q)∨r]⇔[p∨(q∨r)]

b). [(p∨q)∨r]⇔[p∨(q∨r)]

4.- Leyes distributivas.

a). [p∨(q∧r)]⇔[(p∨q)∧(p∨r)]

b). [p∧(q∨r)]⇔[(p∧q)∨(p∧r)]

5.- Leyes de idempotencia.

a). (p∨p)⇔p

b). (p∧p)⇔p

6.- Leyes de Morgan.

a). ¬(p∨q)⇔(¬p∧¬q)

b). ¬(p∧q)⇔(¬p∨¬q)

c). (p∨q)⇔¬(¬p∧¬q)

d). (p∧q)⇔¬(¬p∨¬q)

7.- Contrapositiva.

a). (p→q)⇔(q'→p')

8.- Implicación.

a). (p→q)⇔(¬p∨q)

b). (p→q)⇔¬(p∧¬q)

c). (p∨q)⇔(¬p→q)

d). (p∧q)⇔¬(p→¬q)

e). [(p→r)∧(q→r)]⇔[(p∧q)→r]

f). [(p→q)∧(p→r)]⇔[p→(q∧r)]

9.- Equivalencia

a). (p↔q)⇔[(p→q)∧(q→p)]

10.- Adición.

a). p⇒(p∨q)

11.- Simplificación.

a). (p∧q)⇒p

12.- Absurdo.

a). (p→0)⇒¬p

13.- Modus ponens.

a). [p∧(p→q)]⇒q

14.- Modus tollens.

a). [(p→q)∧¬q]⇒¬p

15.- Transitividad del ↔

a). [(p↔q)∧(q↔r)]⇒(p↔r)

16.- Transitividad del →

a). [(p→q)∧(q→r)]Þ(p→r)

17.- Mas implicaciones lógicas.

a). (p→q)⇒[(p∨r)→(q∨s)]

b). (p→q)⇒[(p∧r)→(q∧s)]

c). (p→q)⇒[(q→r)→(p→r)]

18.- Dilemas constructivos.

a). [(p→q)∧(r→s)]⇒[(p∨r)→(q∨s)]

b). [(p→q)∧(r→s)]⇒[(p∧r)→(q∧s)]

CONTRACCIÒN LOGICA

Definición

Contradicción es una proposición que siempre es falsa para todos los valores de verdad. Para cualquier valor de verdad de las proposiciones, sea cual sea , el resultado de la fórmula lógica estudiada siempre va a ser falso.

Una de las mas usadas y menos compleja es P ∧ ¬P (se lee: P y no P). Su tabla de verdad es la siguiente.

P	¬P	P ∧ ¬P
V	F	V
F	V	V

Ejemplo

• Ejemplo del caso anterior

p: El coche es rojo.

La proposición P ∧ ¬P corresponde a decir que “El coche es rojo y el coche no es rojo”. Por lo tanto se esta contradiciendo o produciendose una Falacia.

Una proposición compuesta en la que los resultados unas veces son 1 y otras 0 en las distintas líneas de la tabla de verdad se denomina Contingencia.